-
复杂生命过程中包含许多的生物化学反应，这些化学反应都具有潜在的随机性，在物理学中，通常用噪声来刻画这些随机性。经典的随机动力系统往往用高斯白噪声来刻画这些随机性。事实上，虽然相比系统自身的时间尺度而言，噪声的自关联时间很小，但是其始终恒大于零，这对系统的相变具有本质性的影响。因此，考虑噪声源的有限关联时间诱导系统的非平衡相变是合理的，考察ComK基因表达系统的动力学瞬态性质和稳态性质具有一定的探索和研究意义。
ComK基因作为枯草芽孢杆菌种群中的看家基因，包含自激活的正反馈环以及一个通过ComS基因介导的负反馈环，耦合调节ComK基因的表达。然而，正负反馈的耦合环路时刻受到外界噪声的刺激，形成内外共振的表达模式，诱导ComK基因表达过程具有自关联时间。据报道，噪声关联强度能够诱导基因表达系统的两种稳定状态在时间延迟下发生切换，增强其稳定性[1]；噪声和交叉关联时间对随机系统的平稳特性有不同的影响[2]；高斯有色噪声及交叉关联时间等随机效应能影响肿瘤免疫反应对化疗系统的稳定性，提高治疗率[3]。文献[4]研究了由乘性色噪声和加性色噪声共同驱动下具有强Allee效应和弱Allee效应的种群模型，对稳定和不稳定状态进行了生物学分析和解释。目前，相关文献均仅涉及色噪声及其交叉关联时间，而对色噪声和自关联时间协同作用下对系统的动力学特性方面的研究尚未见报道。因此，本研究观察ComK基因调控系统在色噪声强度和自关联时间诱导下的非平衡相变现象，着重考察色噪声诱导下基因调节系统的瞬态和稳态变化等的动力学性质，旨在揭示不同源噪声的时间关联性对系统稳态概率分布和平均首通时间的影响。
HTML
-
在枯草芽孢杆菌（Bacillus subtilis）中，转录因子ComK会激活编码DNA摄取和重组系统的基因，会激活自己的正反馈环，多蛋白集合物MecA会降解ComK基因的表达水平,外界刺激会激活ComS缩氨酸竞争的抑制ComK的降解，而ComK的过量表达会抑制ComS的表达，因此，形成正负反馈环路[5-6]。基于此，KARMAKAR和 BOSE[7]提出了ComK基因表达形成ComK蛋白的基因表达模型，该模型中包含ComK转录因子及其复合物、ComK和ComS的相互反馈作用和非线性作用力，其基本机制如图1所示。
Figure 1. Schematic diagram of Bacillus subtilis regulation loop
根据上述模型所示的生化反应，
$x$ 和$S$ 可以表示为：式中，
$a$ 为ComK的蛋白质合成速率，$b$ 为其降解速率，${k_0}$ 为自激活速度，${k_1}$ 为ComS激活ComK的速率，$n$ 为hill系数，$x$ 表示ComK浓度，s 表示ComS压制ComK的速率，$S$ 表示ComS浓度。考虑到ComS激酶相对ComK具有较快的时间尺度，因此，令
$\dfrac{{dS}}{{dt}} = 0 $ ，反带入方程（1），则ComK的蛋白质浓度$x$ 随时间演化的偏微分方程可表示为[8]：当方程
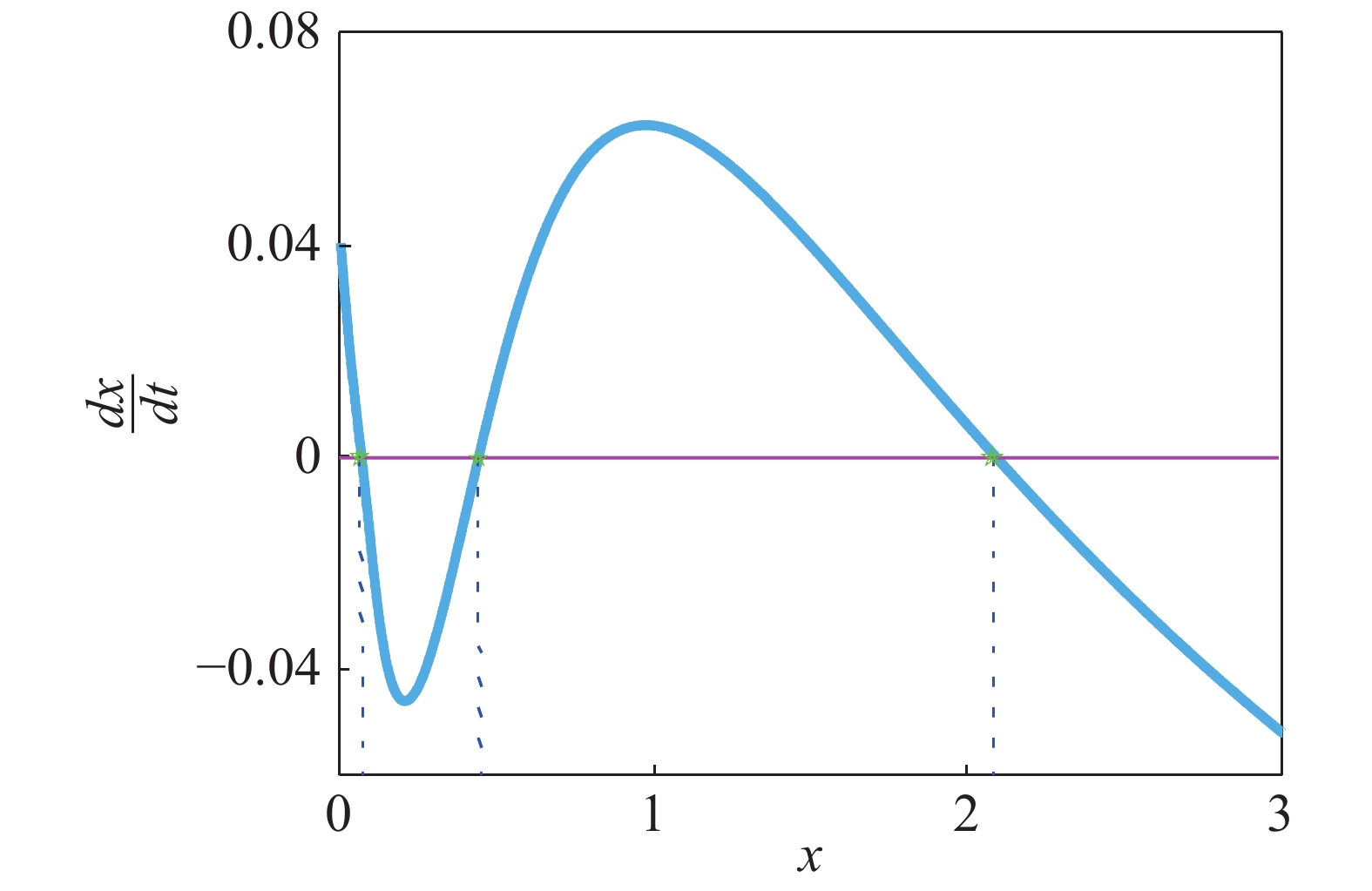
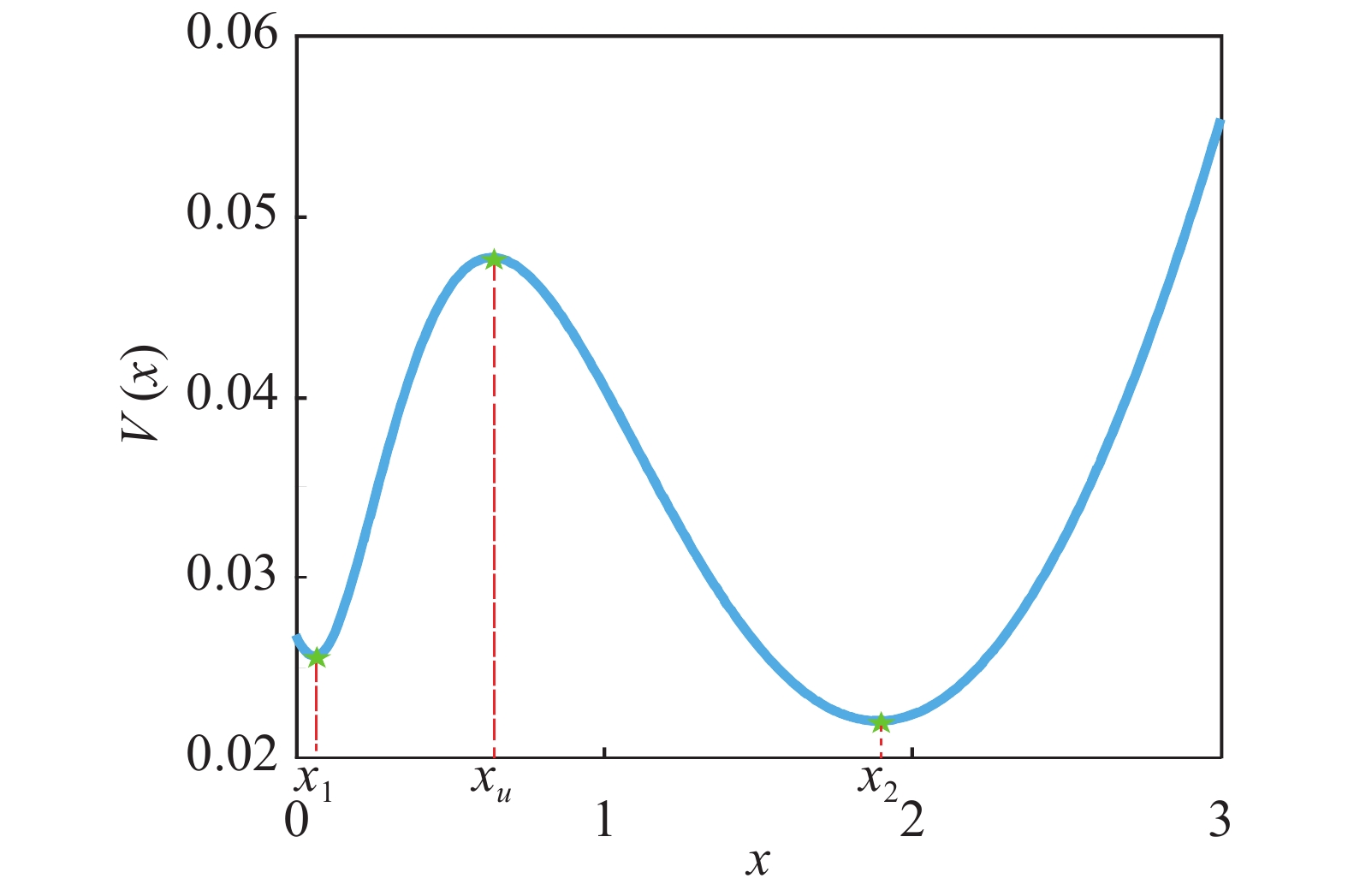
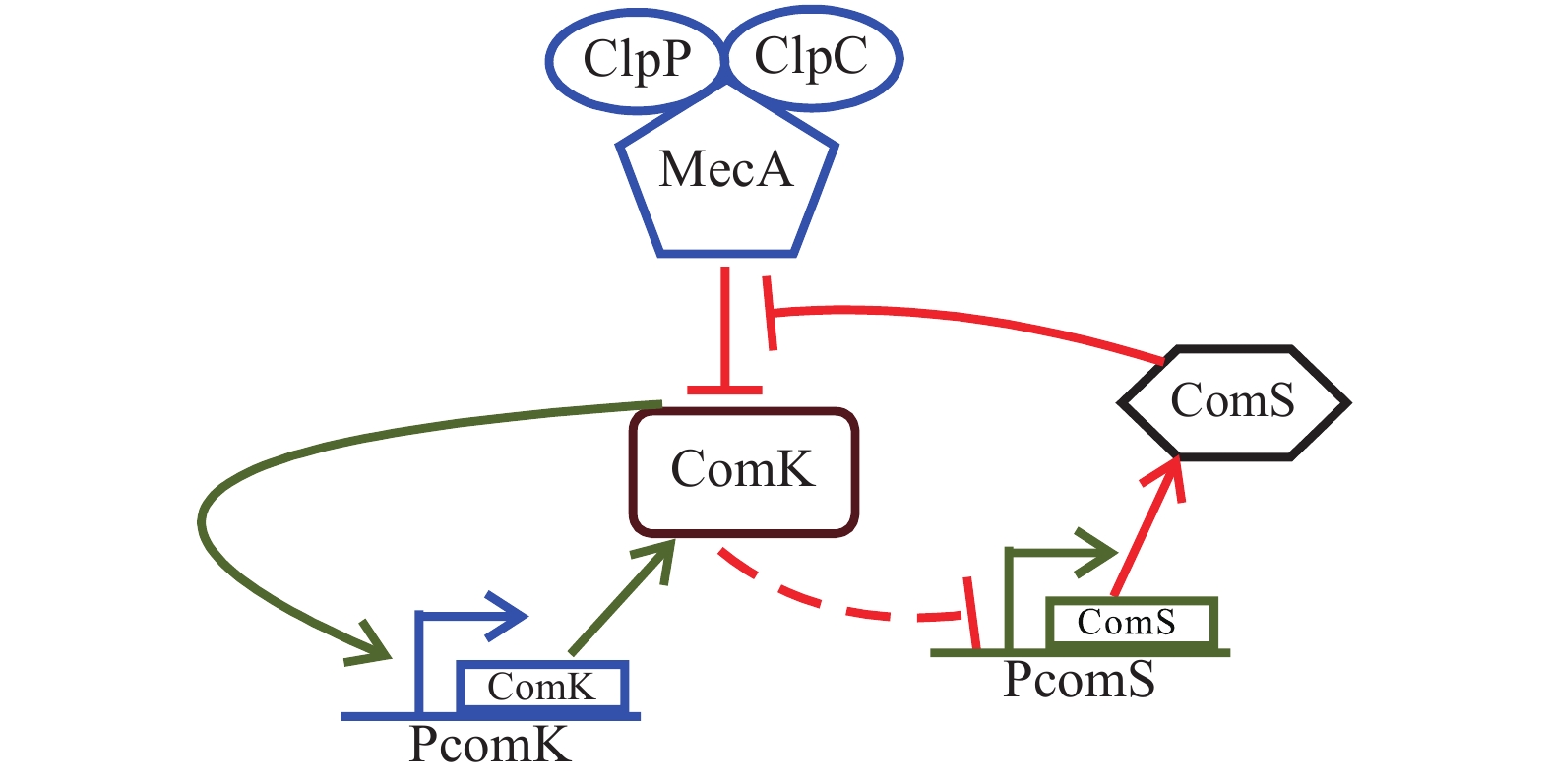
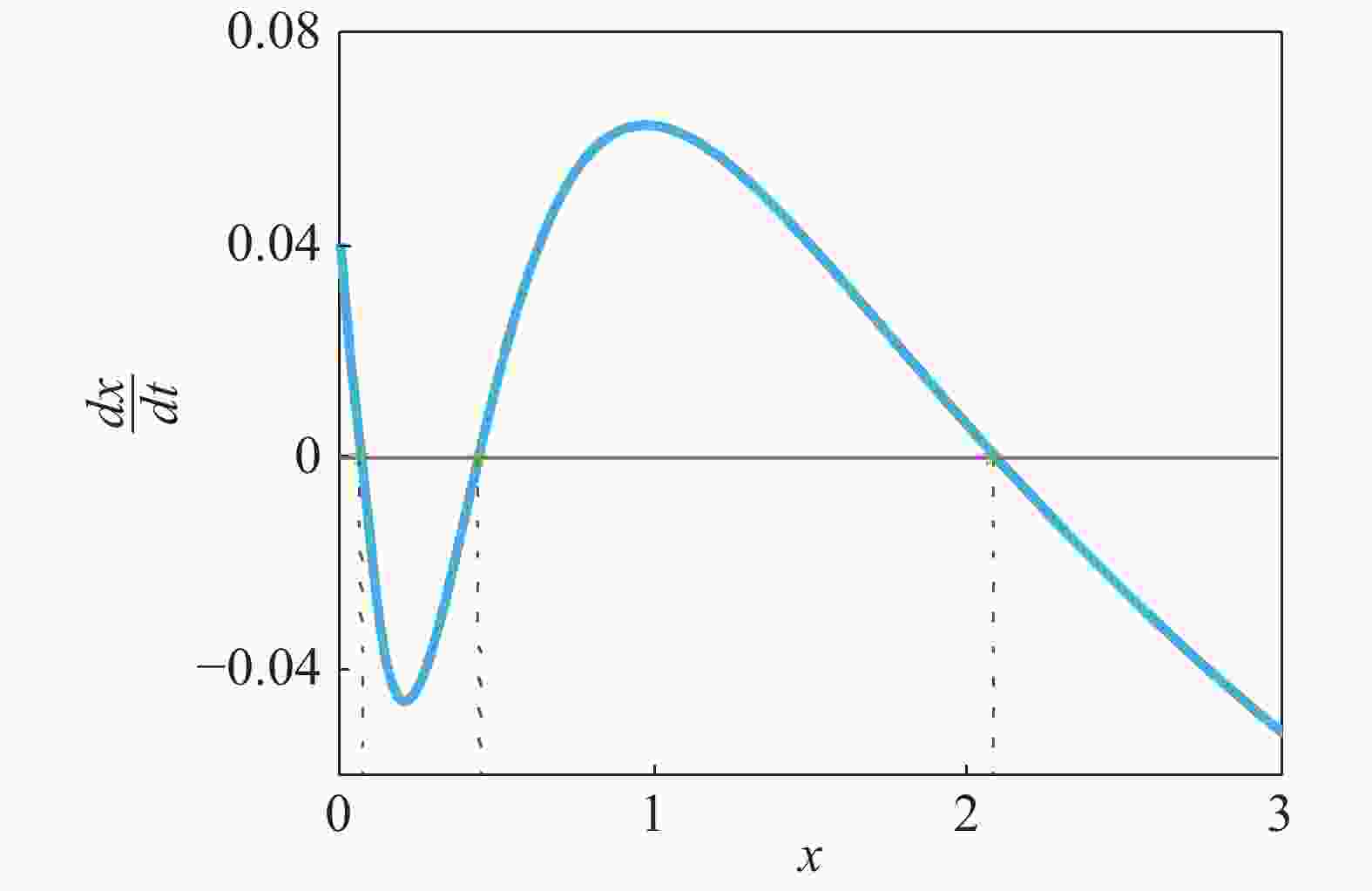
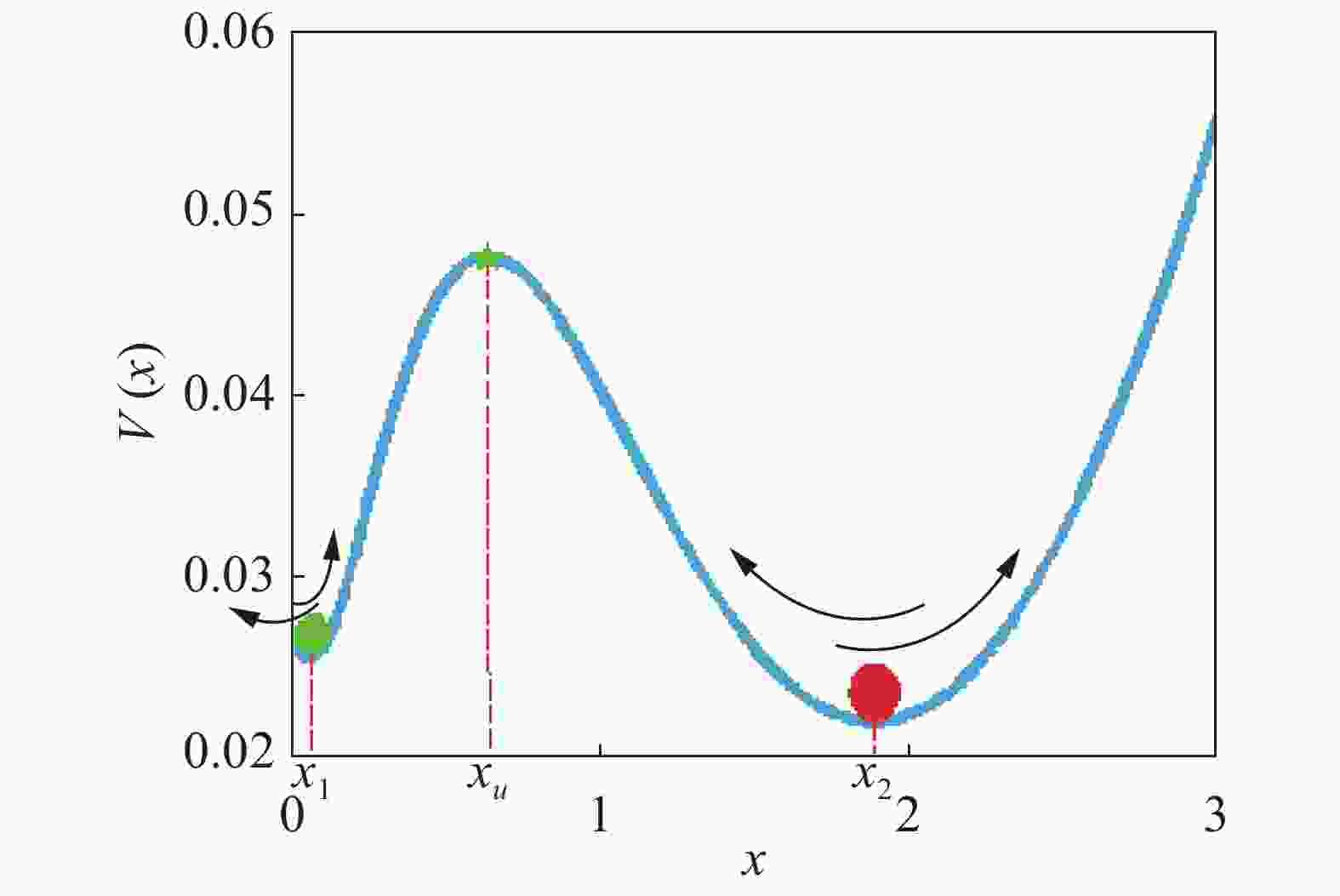
$\dfrac{{dx}}{{dt}} = f(x) = 0$ 具有3个实根，这时系统处于双稳状态，从图2可以看出，该系统包含2个稳态解（$f'({x_i}) < 0$ ），1个低浓度稳定态 (${x_1}$ )，1个高浓度稳定态(${x_2}$ )和1个准稳定态${x_u}$ （$f'({x_u}) > 0$ ），如图3所示，可以清晰的看出该偏微分方程(3)所对应的确定势函数${V_x}$ 的势井图，其中:
Figure 2.
$\dfrac{{dx}}{{dt}}$ as a function of protein concentration$x(t)$ 
Figure 3.
$V(x)$ as a function of protein concentration$x(t)$ 这里，
$f(x) = a + \dfrac{{b{x^2}}}{{k_0^2 + {x^2}}} - \dfrac{{{x^6} - k_1^5(s - 1))x}}{{(1 + x)({x^5} + k_1^5)}}$ 。
-
在KARMAKAR和 BOSE[7]提出的ComK基因表达形成ComK蛋白的基因表达模型的基础上，PAL等[9]在2013年提出了伴随着随机涨落的基本表达模型。根据非平衡系统计算物理和随机过程的相关知识可知，系统的随机涨落与概率函数密切相关[10]，从理论角度出发，主方程可为任何伴随生化反应的系统的概率行为提供建模框架，但是对于一些复杂的网络，特别是非线性系统，要求解主方程的概率函数是很难做到的。因此，基于这一问题，利用概率分布与生成函数之间的关系，重构系统的联合概率函数，推导出以其对应的福克−普朗克方程[11]。在图1模型中，随机涨落在蛋白质的合成率
$a$ 和降解率$b$ 上均有影响，考虑这些因素，引入Gauss色噪声，即$a = a + \eta (t)$ 和$b = b + \varepsilon (t)$ ，则方程（3）重写为朗之万方程：其中，取
$f(x) = a + \dfrac{{b{x^2}}}{{k_0^2 + {x^2}}} - \dfrac{{{x^6} - k_1^5(s - 1))x}}{{(1 + x)({x^5} + k_1^5)}}$ ，${g_1}(x)=\frac{{b{x^2}}}{{k_0^2 + {x^2}}} $ ，${g_2}(x)=1 $ ，则方程（5）具有一般随机动力学机制对应的Langevin方程：
$\varepsilon (t) $ 和$\eta (t)$ 分别是Gauss乘性色噪声和Gauss加性色噪声，它们具有以下所示的统计性质：式中，
$D$ 和$\alpha $ 分别为有色乘性以及加性噪声强度，${\tau _1}$ 、${\tau _2}$ 是分别为其自关联时间。因为蛋白质浓度
$x$ 是一个不可能小于0的值，所以有$x \geqslant 0$ ，这里$p(x,t)$ 用来表示动态蛋白质浓度$x$ 在时刻$t$ 的概率分布函数，因此，朗之万方程（5）对应的$p(x,t)$ 的近似福克−普朗克方程可以应用Novikov定理[12]和Fox近似方法[13]推导出，即概率分布随时间的演化方程为[14]：其中，
$A(x) = a + \dfrac{{b{x^2}}}{{k_0^2 + {x^2}}} - \dfrac{{{x^6} - k_1^5(s - 1))x}}{{(1 + x)({x^5} + k_1^5)}} + \dfrac{{Dx}}{{1 - {\tau _1}{C_1}}}$ ，这里
${x_s} = {x_2}$ 由方程（3）得到，在定态情况下求解方程（8），可以得到其定态概率分布函数为可化简为
式中：
N为归一化常数，
有效势函数
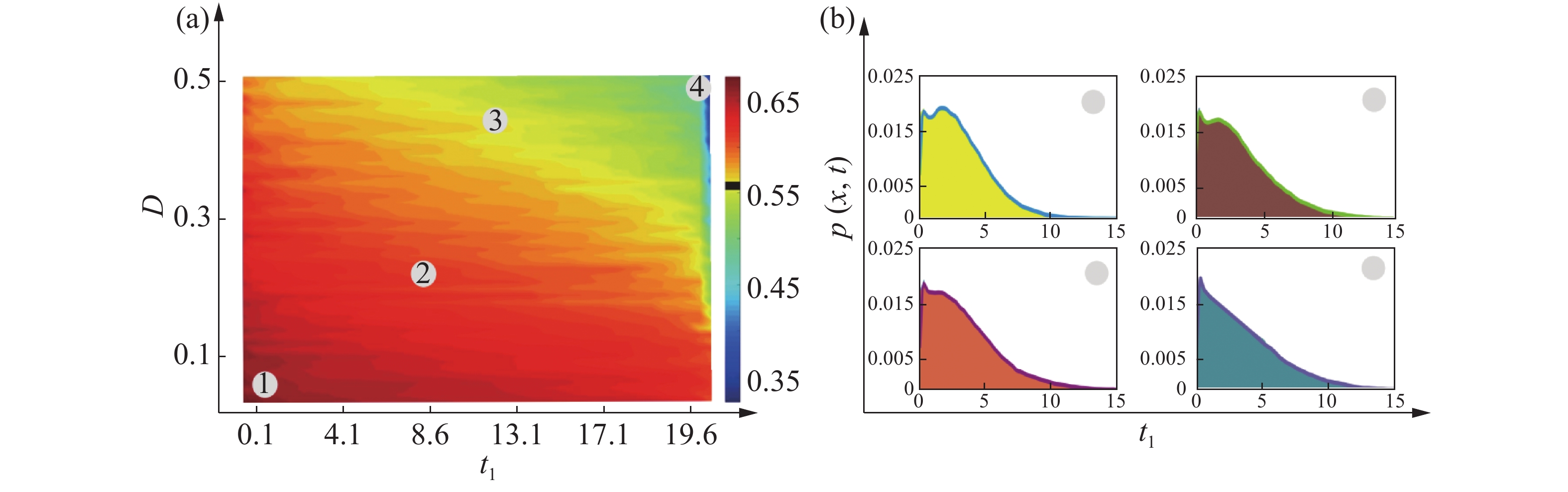
$U(x) = - D\displaystyle \int_{ - \infty }^x {\dfrac{{f(y)}}{{B(y)}}} dy$ 。为了研究色噪声强度和自关联时间对概率分布函数影响，根据有效势函数方程（10）所表达的稳态概率分布函数在基因转录调节系统中的解析式[15]，对方程（10）进行数值计算，在其他参数固定的情况下，做出了不同噪声强度和不同自关联时间的对蛋白质浓度影响的伪三维图，如图4（a） 和5（a）所示，其中，红色区域内均表示该系统处于双稳状态。其他区域表示该系统处于单稳状态，结果表明，系统的稳定性随噪声强度和自关联时间的变化在稳定和不稳定之间变化随着时间的变化，会出现噪声削弱稳定性的现象。为方便讨论，记基因处于高水平表达状态为“on” 状态，反之称为“off ”状态。
Figure 4. (a): Pseudo - 3D diagram of protein concentration at the noise intensity and autocorrelation time; (b): The probability distribution function
${P_{st}}(x)$ is used as a function of the autocorrelation time${t_1}$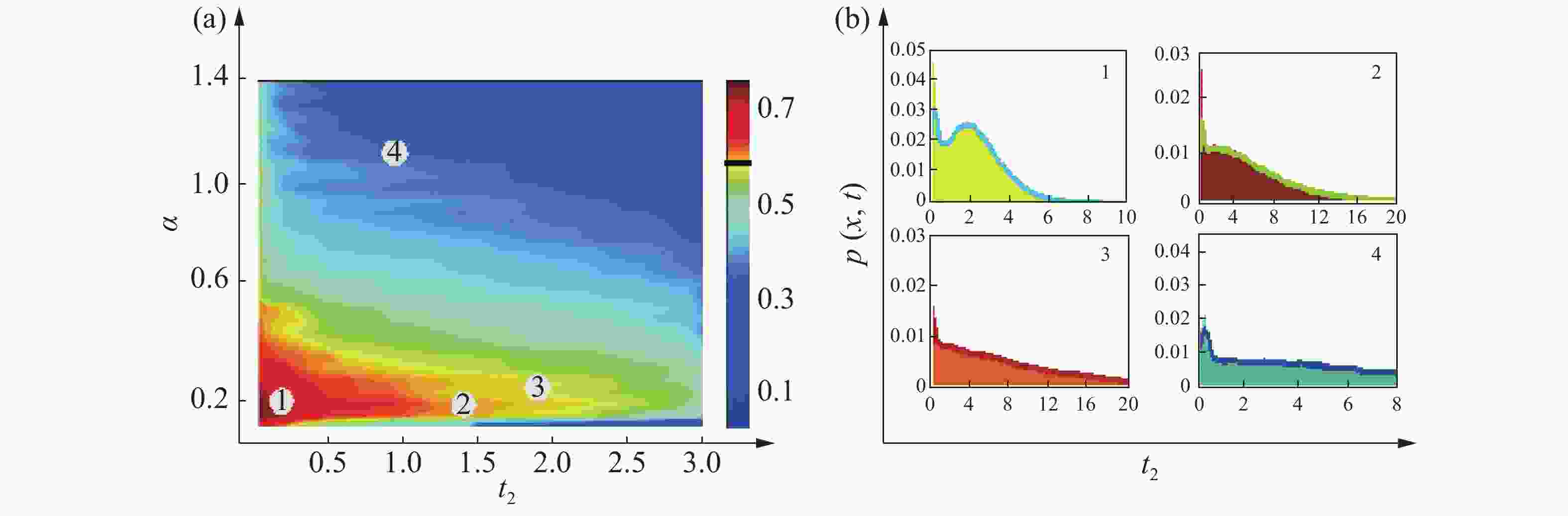 
Figure 5. (a): Pseudo - 3D diagram of protein concentration at the noise intensity and auto correlation time; (b): The probability distribution function
${P_{st}}(x)$ is used as a function of the autocorrelation time${t_2}$ 图4（b）、5（b）给出了概率分布函数不同取值的噪声强度和自关联时间的变化曲线，从4（b）可以看出，随着自关联时间的增大，乘性噪声
$D$ 越大，蛋白质高浓度态逐渐变低，最后消失只剩低浓度态，这说明蛋白质处于失活状态。从图5（b）可以看出，随着自关联时间的增大，加性噪声$\alpha $ 越大，蛋白质高浓度态逐渐变低，最后消失只剩低浓度态，即蛋白质处于“off ”的状态。为了验证方程(5)近似理论解的正确性，进行数值模拟是非常有必要的，应用欧拉算法模拟了朗之万方程(5)和方程(7)，图4（a）和5（a）给出了在不同噪声强度和自关联时间下对蛋白质浓度
$x(t)$ 的时间序列对概率分布函数的影响变化，如图4（b）和5（b）所示，对比近似的理论解和数值模拟得到模拟解，可以看出两个方法的结果基本一致，这就意味着经过考虑噪声强度和噪声的自关联时间来计算该模型对应的福克-普朗克方程得到的理论解是可信的。综合上述，内外噪声强度和其各自关联时间增大，会导致一个稳态随机地失去稳态性，切换到另一个稳定状态，实现状态的切换。因此，得出内外噪声强度和它们的自关联时间可以诱导基因的切换现象，换句话说，可以将噪声强度和自关联时间作为控制基因网络开关切换的参数。
-
双稳系统中噪声会影响两稳态间的相互转化，即系统从一个稳态在外力作用下出发穿越势垒
$\Delta V(x)$ 进入另一个稳态的变化，如图6所示，为得到一个两态间转化的确定时间值，通常用统计的方法[16]，直接考察平均首通时间(MFPT)，可把平均首通时间的精确表达式写成：
Figure 6. The change of the steady state of the system under the action of external force
但方程（11）特别复杂，用一般方法很难处理，因此，在绝热消磁近似的条件下，应用最快下降法[17-18]，在加性噪声强度
$\alpha $ 和乘性噪声强度$D$ 远小于势垒$\Delta V(x)$ 时，利用MFPT的定义和最速下降法可以得到：其中，
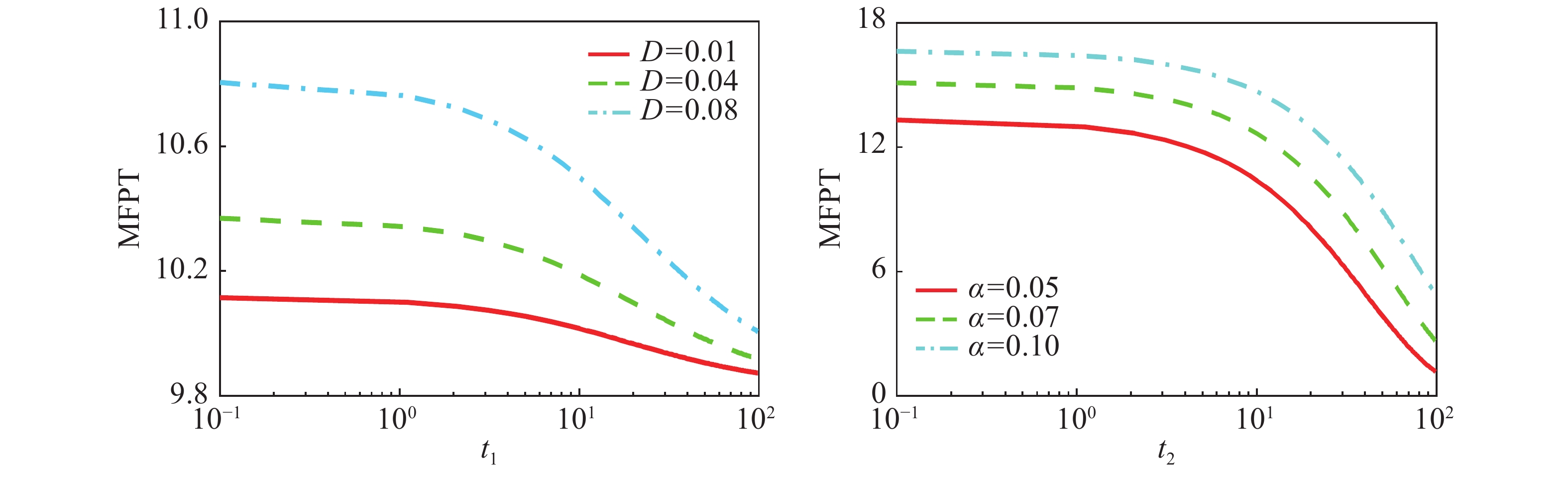
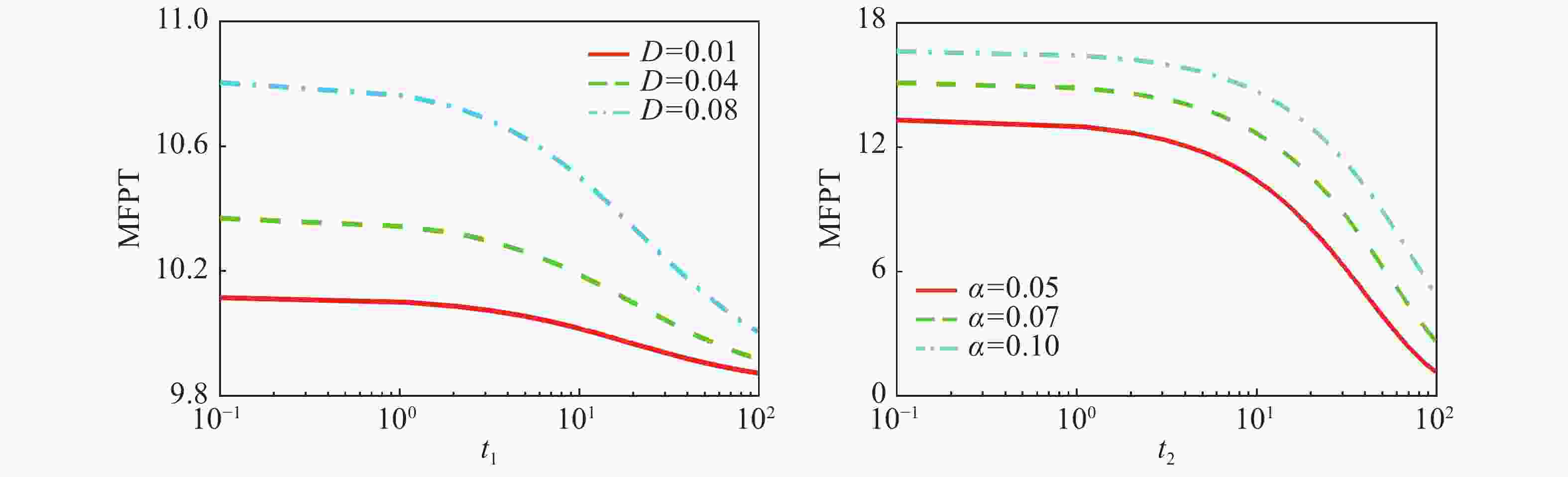
${V_x} = - \displaystyle\int_{ - \infty }^x {a + \dfrac{{b{x^2}}}{{k_0^2 + {x^2}}} - \dfrac{{{x^6} - k_1^5(s - 1))x}}{{(1 + x)({x^5} + k_1^5)}} } dx$ 在基因表达系统中，跃迁是动力学特性中的瞬态性质，而这种瞬态性质常用平均首通时间来刻画，图7（a）给出了在乘性噪声
$D$ 的自关联时间${t_1}$ 下平均首通时间${T_{12}}$ （off态${x_1}$ 跃迁到on态${x_2}$ ）的函数图像，在不同乘性噪声强度下，MFPT会随着${t_1}$ 的增大呈现出单调递减的趋势，图7（b）给出了在加性噪声$\alpha $ 的自关联时间${t_2}$ 下平均首通时间${T_{12}}$ （（off态${x_1}$ 跃迁到on态${x_2}$ ）的函数图像，在不同加性噪声强度下，MFPT会随着${t_2}$ 的增大呈现出单调递减的趋势，这说明，随着自关联时间${t_1}$ 和${t_2}$ 的增大，噪声强度越大，蛋白质浓度从低浓度态转向高浓度态所需要的时间越少，即从“off ”状态到“on”的转换变得越容易，即加速了状态之间的转化，换句话说，自关联时间会削弱高蛋白质浓度态的稳定性。
Figure 7. The change of the mean first passage time (MFPT) of the system under the influence of color noise autocorrelation time
-
本研究应用诺维科夫理论和福克斯近似方法给出ComK基因表达系统中稳态概率分布函数的近似表达式，分析了色噪声诱导蛋白质浓度转换的现象以及该系统动力学特性中的瞬态性质，通过分析可以得到以下结论：噪声强度及其自关联时间的变化会影响概率分布函数曲线的峰值位置、峰值个数的变化，即噪声强度及其自关联时间确定会影响系统发生相变。在不同乘性噪声和加性噪声的噪声强度下，随着自关联时间的增大，蛋白质从低浓度态跃迁至高浓度态所需时间减少，加速了状态之间的转化，说明噪声强度和自关联时间会引起蛋白质的浓度经历了“开”→“关”的转换，即自关联时间在一定程度上会削弱蛋白质浓度态的稳定性，表明不同源噪声的自关联时间能诱导ComK基因在各种表型状态之间切换，提高其生存概率。通过分析影响基因调节系统中蛋白质浓度转化的因素和噪声强度对系统的影响，发现蛋白质浓度转化的一般规律和噪声强度及自关联时间的大小对系统产生的影响。本研究为基因方面的药理学研究提供了一定的理论方法。
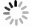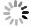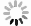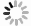
DownLoad:
