-
海南岛地处热带北缘,属热带季风气候,是地球上同纬度降雨量最多的地区之一[1]。海南岛秋季降水约占年降水量的37.6%,是暴雨出现频次较高的季节,且易出现连续暴雨天气过程[2]。海南岛秋季连续暴雨常造成洪涝、城市内涝、泥石流等灾害,造成严重的经济和人员损失。如何及时定量获取秋季暴雨的空间分布,为政府部门的防洪救灾决策提供帮助,成为近年来气象科研人员关注的重点领域之一。雨量计、雷达和卫星是目前测量降雨的3种最主要手段。雨量计作为传统的测雨工具,其观测量常被认为是真实的或者参考的降雨值。然而,雨量计分布的不均匀或者空间覆盖率的不足会导致在估算面雨量时容易出现较大偏差,尤其是在山区和流域周围[3]。利用卫星观测雨量是一种很具吸引力的方式。卫星观测能提供全球尺度的降雨量,但很难提供小尺度和实时的雨量数据。此外,随着时间尺度的减小(即从月到日到小时),卫星估测降雨的精度也随之降低[4]。雷达定量估测降水是通过建立雷达回波与雨量计测雨值之间的关系,得到较大范围内高时空分辨率的降雨场,在一定程度上弥补了雨量计和卫星观测的不足[5]。
在利用雷达估测降雨中,Z-R关系被广泛应用。雷达反射率因子Z与雨量计实测雨强R的配对方法是影响Z-R关系精度的关键因素。CALHEIROS等[6]假设雨滴从大气下降到雨量计的过程绝对垂直且耗时为零,即匹配同一时刻且正垂直的雨量计实测量R和雷达实测值Z,这就是传统的Z-R配对方法(the traditional matching method, 简称TMM法)。TMM法物理过程清晰,简单易行,是最基本匹配法之一。在TMM法的假设未考虑现实中Z、R数据集存在的时空不匹配问题,而这恰是影响Z-R关系准确性的关键因素。因此,ATAS[7]、ROSENFELD[8]提出概率配对法(the probability matching method, 简称PMM法),假设雷达反射率因子Z与雨量计实测量R具有相同的发生概率,即可用概率密度函数把Z、R匹配起来,进而建立Z-R关系。ROSENFELD[9]进一步提出了窗口概率配对法(the window probability matching method, 简称WPMM法),旨在减少概率配对法中的时空不匹配问题。PMM和WPMM法的基本假设是一致的,通过寻找基于雷达反射率Z对雨量计实测降水R的一种概率密度函数,建立Z-R关系。其缺点在于匹配中未能再现降雨的真实物理过程,而优点也在于匹配过程中几乎不需要考虑R和Z之间的物理联系以及同步性,具有较强实用性且估测精度较高。PIMAN [4] 提出窗口相关配对法(the window correlation matching method, 简称WCMM法),寻找最优Z-R配对,试图解决雷达观测高度与风的客观存在导致Z、R配对时的时空不匹配问题。WCMM法在泰国的应用情况显示WCMM法的估测精度较TMM法、PMM法和WPMM法有不同程度的提高[10]。该方法采用1个小的滑动时空窗并应用相关关系匹配Z-R对,在一定程度上解决了Z、R配对时的时空不匹配问题,但计算相对复杂,计算机资源需要较大。
中国基于雷达反射率和雨量计进行降水估测的研究很多。李腹广等[11]基于TMM法,利用兴义多普勒雷达体扫复合仰角资料进行降水估测,结果表明,所得Z-R关系适用性较好,准确率较高。吴星霖等[12]基于TMM法本地化邵通地区的Z-R关系,小时降水估计的拟合率约80%。郑嫒媛等[13]根据雷达不同距离段不同仰角PPI资料与雨强,建立概率配对序列,得到安徽地区的Z-R关系。张爱民等[14]利用安徽合肥S波段多普勒雷达进行降水估测,结果表明,PMM法的表现优于最优化法,24 h站点雨量平均相对误差均小于40%。高晓荣等[15]利用PMM法对广东的6部多普勒雷达估测降水,再进行降水估计拼接,以此来扩展降水估计范围。邵月红等[16]通过改进的最佳窗概率配对法(WPMM法)、遗传算法和最优化法分别得到沂沭河流域多普勒雷达降水Z-R关系,对比结果表明,改进的最佳窗概率配对法估测结果最优。目前国内尚无基于WCMM法进行定量估算降水的文献。另一方面,受到降雨分布,雨滴谱特征、近地面气流、区域特点等因素的综合影响,Z-R关系具有很强的区域性,如何使其本地化是一个待解决的问题。目前,海南岛秋季暴雨的雷达定量降水估测方面的工作还较少,笔者采用TMM、PMM、WPMM和WCMM 共4种配对方法同时进行降水估测试验,改进海南岛地区多普勒雷达降水产品的性能,以期获得更精准的秋季降水定量估测产品。
-
采用海口CINRAD WSR-98D雷达,位于19°59′47″N,110°14′45″E,海拔118 m。收集2017年和2018年9—11月逐6 min 1次的多普勒雷达体扫资料。
对雷达基本反射率数据进行处理,主要包括以下几个方面:(1)数据的方位统一 :为了方便进行不同仰角数据的比较 ,将每个仰角的数据统一插值到 0~359°的方位角上[17];(2)假定引起降水的最小反射率因子为21 dBz[13],小于该强度的回波认为是非降水事件;(3)将>55 dBz的反射率因子,令其为55 dBz;(4)为避开地物杂波干扰,距雷达0~60 km采用3.4°仰角,60~120 km采用1.5°仰角,120~230 km采用0.5°仰角。
-
收集海南省490个气象观测站2017年和2018年9—11月逐5 min自计雨量资料。本研究所使用各气象台站的雨量计多为虹吸式雨量计,其精度为0.1 mm。考虑到雷达体扫间距与雨量计观测间距的不匹配,将雨量资料插值成6 min间隔的数据。本研究选取的雨强阈值为0.6 mm·h−1,即不考虑0.6 mm·h−1以下的降水。
从收集的雨量计数据中选取出19个强降水事件(共23 d),其中2017年10个,2018年9个。强降水事件的定义:在降水时段内观测到强降水(>50 mm·6 h−1或者>20 mm·h−1)的市县达3个以上。
-
TMM法为匹配同一时刻且正垂直的雨量计实测量和雷达实测值。本研究把1 h雨量计降雨量R和同一时段的垂直于雨量计的平均雷达反射率因子值Z,配成1个Z-R对。在得到若干Z-R对后,利用最小二乘法拟合得到Z-R关系式,可用公式(1)表示(本研究所有配对法所得Z-R关系式将统一使用该式表示):
式中,Z是以mm6·m−3为单位的雷达反射率,R是以mm·h−1为单位的降雨强度,a和b为参数。此外,
$d B z=10 \lg 〔 Z 〕 ; d B R=10 \lg 〔 R 〕 $ 。 -
在TMM法中假设,雨量计测量的降雨量与雨量计正上方的雷达反射率是同步的。然而,现实中该假设几乎是不存在的。原因:(1)地面雨量计附近雨滴谱分布与雷达有效照射体积的空间不一致;(2)雷达波束的平均作用;(3)雨量计测量和雷达测量的时间、地点上的不一致。为了消除Z、R之间的时空不匹配,CALHEIROS等[6]、ATLAS等[7]提出PMM法,假设在气候均匀的区域内,雷达反射率因子Z与雨量计实测量R是描述降水事件的2个随机变量,具有相同的发生概率。任一点任一时刻雨强R的发生概率为
$\mathrm{P} 〔 R 〕 \mathrm{d} R $ ,雷达反射率因子Z的发生概率为$ \mathrm{P} 〔 Z 〕 \mathrm{d}Z$ ,若Z和R 2个随机变量一一对应,那么必有$\mathrm{P} 〔 R 〕 {\rm{ d}} R=\mathrm{P} 〔 Z 〕 \mathrm{d}Z $ ;反之,若已知Z和R的概率分布,那么依据概率相等原理即可决定Z-R关系。PMM法消除了定时误差,因为PMM法没有利用每对R和Z发生的实际时间,并且只要雨量计上雷达像素处的雨滴绝对垂直,PMM法就间接消除了几何误差。通常,对累计雨量贡献很小的雨强常占有相当大的概率,为了减少小雨强事件的干扰,为此,ATLAS[6]建议用公式(2)配对:
公式(2)增大了大雨强和大反射率的影响,对
$Z_{{\rm{c}}} $ 阈值$R_{i} $ 和选取不太敏感。按CDF1相等原理,得到一组$Z_{i}\text{-}R_{i}$ 对的序列,利用最小二乘法拟合即可得到气候Z-R关系。公式(2)中的$Z_{c} $ 和$R_{c} $ 分别为21 dBz和0.6 mm·h−1。 -
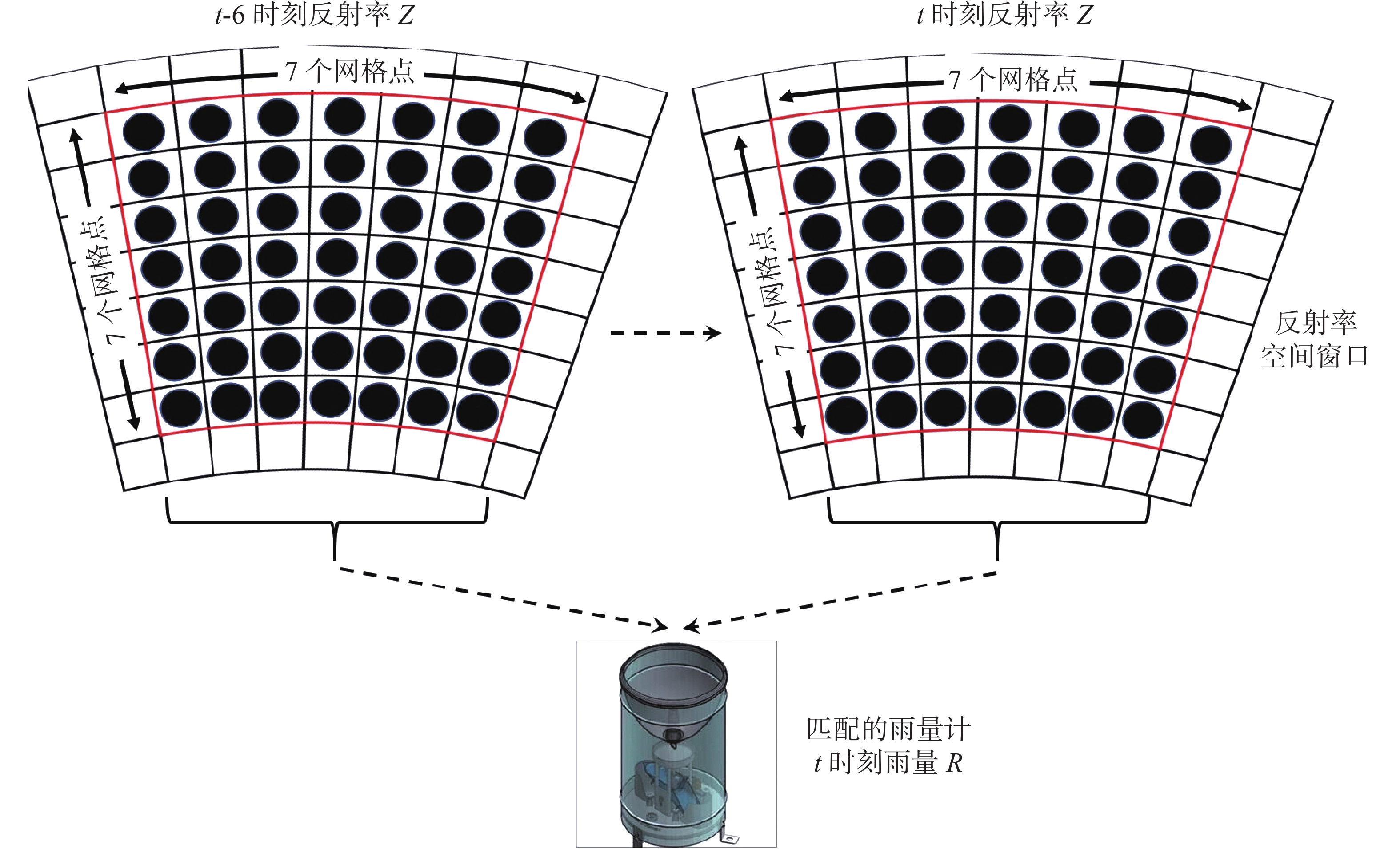
为了减少Z和R在匹配中的几何失配和同步误差,ROSENFELD等[9]发展了WPMM法。WPMM法考虑到雨滴从雷达像素处下落到雨量计需要时间,且雨滴在下落过程中并不垂直。因此,可通过将雨量计测量的降雨强度匹配仅从围绕雨量计中心的小窗口(时间和空间)获取的雷达反射率来消除时空误差。该窗口必须足够小,以便雨量计能够表示雨量计上方雷达窗口内的降水量度,但要足够大,以包含此类测量固有的时间误差和几何误差。本研究选择使用以雨量计为中心的空间窗尺寸7×7的雷达网格(共包含49个雷达反射率因子),以及3个6 min时间窗口的雨强值。如图1所示,其中Z从空间窗口获得,位于雨量计坐标的中心,R从雷达扫描时中心的3个6 min平均雨量计强度中获得。为了得到1个无时间误差的代表性PDF(R),必须包含前一个和后一个6 min的雨强度。因此,每个雷达扫描和每个雨量计分别为PDF(Z)贡献49个Z值和为PDF(R)贡献3个R值(包括零值)。通过WPMM法匹配,可以获得雷达和雨量计观测之间较接近的同步,并且可以确保高空的雷达观测与地面的雨水测量相对应,从而减少因风吹动雨滴导致的Z、R匹配时存在的误差。该匹配方法能增加Z-R对的数量(相对PMM法),对提高估计的Z-R关系的精度有帮助[9]。
计算WPMM的Z-R关系为拟合从所有窗口获得的通过无条件累积概率匹配得到的Z-R对。把来自同一窗口的Z和R两个数据集(每个窗口提供49个Z和3个R值)排序;具有相同累积百分位数的Z和R是相互关联的,这样每一个雨量计可提供若干个Z-R对;最后利用范围内所有雨量计提供的Z-R对求解出Z-R关系式。
-
为了减少降雨过程中由风和雷达测量高度引起的Z-R配置错误和定时错误(非同步的Z-R数据集),PIMAN等[4]提出了WCMM法。WCMM法与WPMM法在物理假设上是相近的,主要区别在于Z和R数据集的处理上。WCMM法使用非同步的Z和R数据集来建立具有代表性的反射率−雨强关系。该方法的概念是对传统配对方法中搜索和寻找与R具有最佳对应关系的最优匹配区域的扩展。
WCMM法的匹配过程(图2)包括将空间和时间窗内的Z值与参考雨量计的降雨强度R进行匹配,搜索出雷达反射率因子Z值,使得Z和R之间的相关性达到最大,其中相关系数r根据公式(3)和公式(4)求得。将该Z值指定为与参考雨量计的降雨强度R匹配,这对Z-R被称为“最优Z-R对”。
式中,
$Z_{i} $ 是非零Z-R对数据集中第i个Z值,Z是Z的平均值,Ri是非零Z-R对数据集中第i个R值,$\overline R $ 是R的平均值,$S_{Z} $ 是Z的标准偏差,$S_{R} $ 是R的标准偏差,n是所计算雨量站若干小时内的非零Z-R对个数。根据前人的研究结果[4],使用空间窗尺寸7×7的雷达网格,并结合当前时间和前6 min雷达扫描时间窗口,可以纠正Z-R对中的配置和定时错误,因此本研究沿用该配置(简称S77T6配置)。S77T6配置中,为了寻找最优Z-R对,每个站点的每个R值需要匹配98个Z值(需要匹配前后两个雷达窗口的网格点:7 × 7 × 2)。另外,考虑到计算量的问题,本研究选取实测雨强的变化范围为6~90 mm·h−1,增量为6 mm·h−1。
-
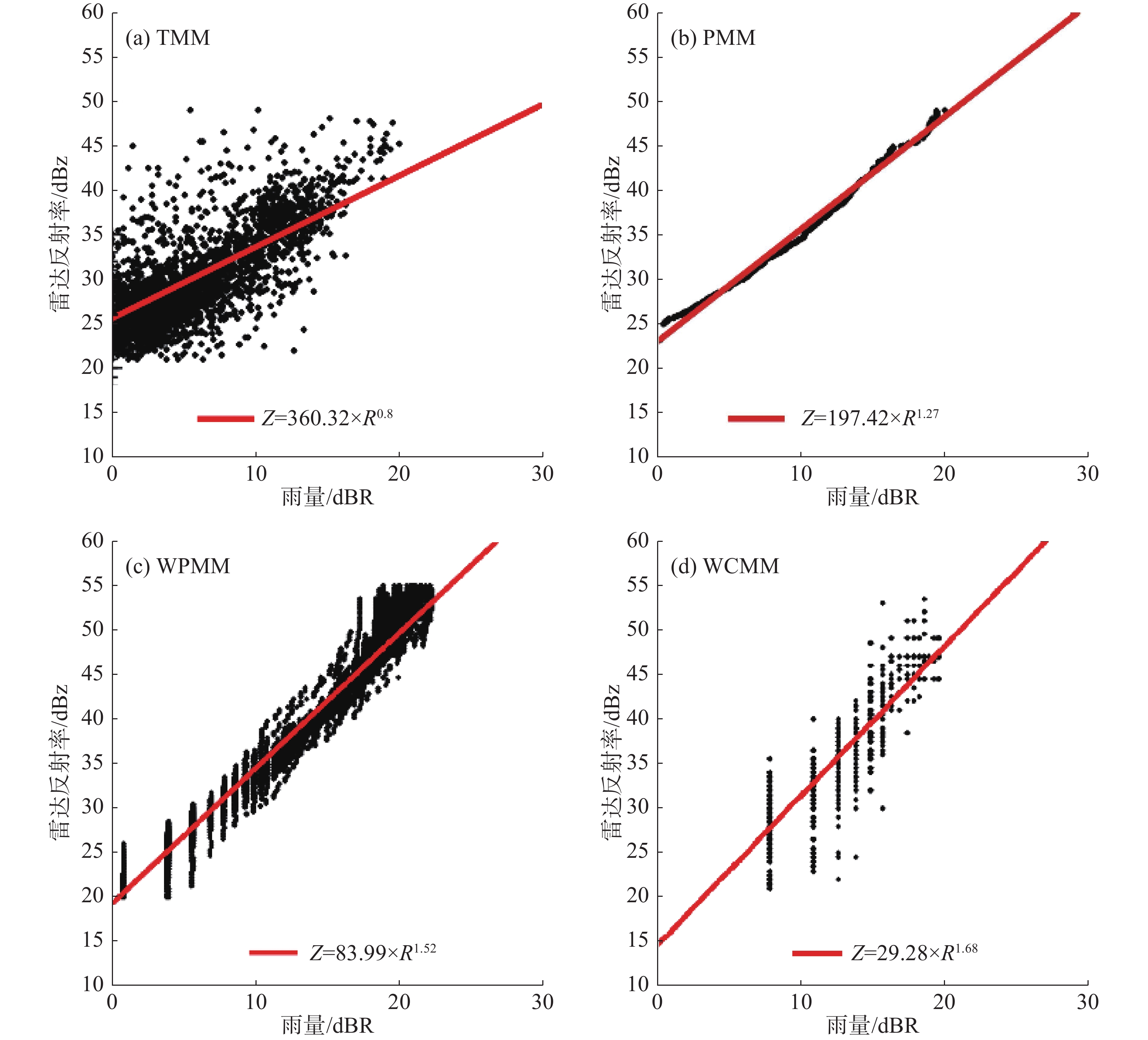
利用TMM、PMM、WPMM和WCMM 4种配对法分别获得各自的Z-R对,通过最小二乘法线性拟合回归求得a、b参数值,得到不同区域的气候Z-R关系(a、b参数的详细分布见表1)。
距离/km Z-R关系式参数 TMM PMM WPMM WCMM a b a b a b a b 0~<30 360.32 0.80 197.52 1.27 83.99 1.52 29.28 1.68 30~<60 365.11 0.66 143.56 1.41 64.22 1.53 18.7 1.90 60~<90 375.14 0.69 147.53 1.38 78.36 1.47 52.87 0.75 90~<120 397.61 0.64 135.10 1.41 82.26 1.46 49.32 0.70 120~<150 379.37 0.57 106.76 1.47 71.67 1.47 65.61 0.55 150~<180 374.66 0.53 145.80 1.29 98.60 1.34 43.14 0.81 180~<210 414.76 0.35 204.52 1.02 106.79 1.24 18.83 1.14 210~<230 421.52 0.35 217.95 1.02 100.72 1.26 73.49 1.03 为了评估不同区域Z-R配对的合理性,对不同区域的4种Z-R对绘制散度图及拟合直线,结果如图3所示(仅展示距雷达0~<30 km范围的情况,其他区域相类似)。TMM(图3-a)、PMM(图3-b)、WPMM(图3-c)和WCMM(图3-d)分布匹配的Z-R对(黑色散点)大致均匀分布在拟合直线(红线)两侧,表明4种配对法拟合的Z-R函数可以较好描述Z-R对的分布,尤其是PMM法所得拟合直线几乎与Z-R对分布重合,拟合效果最好。
-
表2给出了4种配对法所得小时雨量的绝对误差和相对误差,加粗的数值表示绝对误差小于0。对于小时雨强(<5 mm·h−1)事件,4种配对法对QPE的反演都存在明显的高估,随着雷达探测距离的增长,高估程度趋于增大,210~<230 km的相对误差可达725.3%(WCMM)。PMM法对小雨强事件的高估程度在4种方法中最低,0~<30 km的误差为1.9 mm,相对误差为94.1%。4种配对法对中等雨强(5~20 mm·h−1)事件的反演的相对误差较小雨强(<5 mm·h−1)事件有所降低。PMM和WPMM法所得时雨强存在低估,WCMM法和TMM法存在高估。PMM法和WPMM法的相对误差明显小于其他两种配对法,反演结果更接近实况。对于大雨强(>20 mm·h−1)事件,4种配对法的反演大多为低估,PMM法和WPMM法低估的程度(相对误差)小于TMM法和WCMM法。总之,4种配对都有着对弱降水事件估测偏大,强降水事件估测偏小的倾向;PMM法和WPMM法的小时雨强反演效果更好,更接近实况。
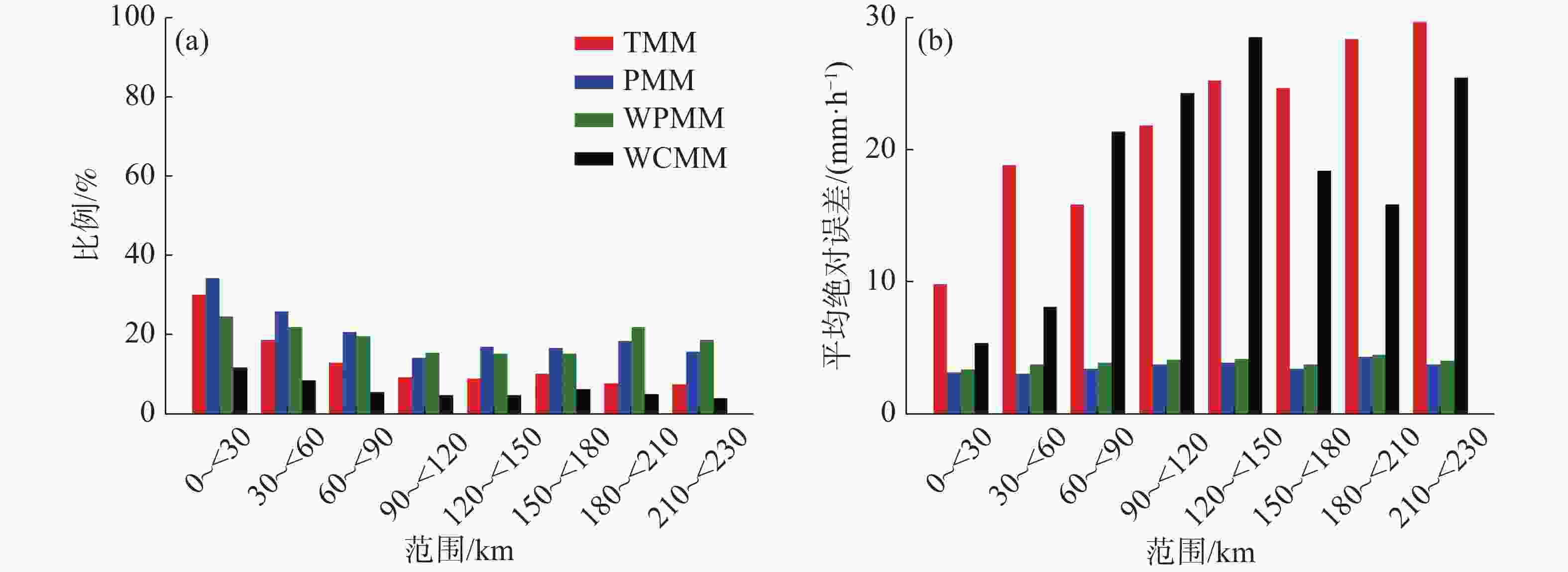
距离/km TMM PMM WPMM WCMM <5 5~20 >20 <5 5~20 >20 <5 5~20 >20 <5 5~20 >20 0~<30 5.2 14.1 17.8 1.9 −0.8 −16.5 3.1 0.7 −15.3 6.0 5.8 −8.0 253.8 133.5 52.8 94.1 7.1 48.9 153.9 6.3 45.5 295.6 54.5 23.7 30~<60 10.2 14.5 17.1 2.2 −2.5 −21.2 4.2 0.3 −17.9 9.7 7.6 −30.0 497.7 262.4 58.1 102.3 26.9 72.0 192.8 3.4 60.9 446.6 81.0 134.1 60~<90 11.8 7.9 −33.6 2.5 −4.1 −28.0 4.2 −2.3 −26.5 11.7 22.6 −54.1 541.1 86.8 105.5 110.6 44.7 87.9 184.9 25.2 83.2 537.0 248.8 169.8 90~<120 8.5 6.5 −40.0 3.5 −5.6 −31.7 5.2 −4.4 −30.9 6.9 33.3 −41.9 407.4 70.4 119.1 170.2 60.4 93.2 251.6 47.6 90.8 322.0 356.9 124.4 120~<150 7.4 19.3 −48.1 3.5 −5.8 −27.1 5.2 −4.5 −25.8 8.7 44.4 −74.7 329.9 193.5 153.9 173.6 58.2 86.7 258.8 45.1 82.5 422.9 445.9 254.3 150~<180 8.2 7.7 −33.0 3.4 −5.8 −26.7 4.6 −4.8 −25.9 9.1 43.3 10.8 469.2 82.1 111.2 172.5 61.3 90.0 237.0 51.3 87.3 521.1 460.4 36.3 180~<210 10.6 13.4 −35.6 3.4 −3.9 −21.1 4.0 −3.1 −21.0 12.1 25.3 −24.1 553.7 180.9 126.1 167.9 41.9 71.2 198.5 33.6 70.9 684.4 271.8 91.2 210~<230 15.2 11.6 −27.2 7.4 1.8 −26.7 7.5 1.4 −25.5 17.6 33.7 −30.4 692.7 121.3 94.4 384.9 18.6 92.8 391.5 14.8 88.5 725.3 349.9 122.1 注:(1)表中带底色部分为绝对误差,公式:AE = QPE−OBS,单位为mm; (2)表中无底色部分为相对误差,公式:$RE = \dfrac{ {\left| {QPE - OBS} \right|} }{ {OBS} } \times 100\text{%}$;(3)表中加粗部分表示绝对误差小于0。 从估测小时雨强|相对误差|≤20%的个数在所有样本中所占比例分布柱状图(图4-a)可以看出,随着离雷达位置越远,比例呈下降趋势,估测降水的相对误差在增大。PMM法估测降水的表现最好,估测降水相对误差较小,比例在30%~40%之间,其次为WPMM法。在平均绝对误差(MAE)方面,MAE也随距离的增加而增大(图4-b)。PMM法的MAE都在4 mm·h−1以下,是4种方法中最小的。说明PMM法估测单点降水能力较TMM法、WPMM法和WCMM法强。
-
为了更全面评估4种配对法的估测结果,本研究计算区域范围内雨量计所有降水量之和及相应站的估测降水量总和。表3给出了2017—2018年秋季区域总雨量实况与4种配对法估测降水的对比,可以看到TMM法、WPMM法和WCMM法在面雨量上都存在不同程度的高估,并且距离雷达越远,高估程度越大。PMM法在距雷达60~<180 km的范围内出现面雨量低估,其余范围内为高估。在0~<60 km和150~<230 km范围内,PMM法的面雨量估测精度最高,在0~<30 km范围内仅偏差了324 mm,占实测面雨量的2.1%。60~<150 km范围,WPMM表现最佳,偏差均小于15%。
距离/km 实测雨量/mm 估测雨量 TMM PMM WPMM WCMM 偏差/mm 比例/% 偏差/mm 比例/% 偏差/mm 比例/% 偏差/mm 比例/% 0~<30 15 726 21 021 133.8 324 2.1 3 588 22.8 13 156 83.7 30~<60 12 362 59 657 482.6 759 6.1 6 458 52.2 21 865 176.9 60~<90 24 943 53 877 216.5 −3 819 −15.3 3 669 14.7 6 288 252.1 90~<120 21 104 65 973 312.6 −4 434 −21.0 699 3.3 8 777 415.9 120~<150 12 813 104 115 812.6 −2 229 −17.4 1 067 8.3 9 863 769.8 150~<180 14 658 118 740 810.1 −778 −5.3 2 576 17.6 10 975 865.3 180~<210 4 412 4 077 952.1 1 269 28.8 19.24 43.6 5 132 1 163.3 210~<230 1 085 1 230 1134.5 1 146.7 105.7 1 171 108.0 1 678.7 1 547.2 -
本研究利用4种方法分别求解海南岛秋季的区域气候Z-R关系,对秋季暴雨过程进行雷达定量降水估测,并与雨量计实测降水进行比较,可以得到以下结论:
(1)4种配对都存在对弱降水事件估测偏大,强降水事件估测偏小的倾向。估测降水的效果随雷达探测距离的增大而下降。
(2)在小时雨强评估中,PMM法的平均绝对误差和相对误差都是4种方法中最小的,表明PMM法估测单点降水能力较TMM法、WPMM法和WCMM法强。
(3)在面雨量评估中,PMM法估测面雨量在0~<60 km和150~<230 km范围内偏差最小,WPMM法则在60~<150 km范围内表现更优。
(4)总体上看,PMM法在小时雨强和面雨量估测两方面较其他3种方法具有明显优势,可利用PMM法得到的Z-R关系调整海南雷达估测降水,形成更稳定更精准的雷达定量估测降水产品。
本研究仅利用海口CINRAD WSR-98D雷达资料对2017—2018年海南秋季强降水过程进行分析,所得结论具有一定的局限性和时空独特性。今后可进一步对更多年份的秋季强降水过程进行检验分析,并对海南的台风降水、午后强对流降水等过程进行对比分析,以便得到普适性更高,更有价值的结果,从而切实提高海南地区降水的定量估测能力。
Comparative experiment of several quantitative precipitation estimation techniques based on doppler radar over the Hainan Island during autumn
doi: 10.15886/j.cnki.rdswxb.2022.04.006
- Received Date: 2021-09-24
- Accepted Date: 2022-06-09
- Rev Recd Date: 2022-03-25
- Available Online: 2022-06-13
- Publish Date: 2022-07-26
-
Key words:
- quantitative precipitation estimation(QPE) /
- probability matching method(PMM) /
- window probability matching method(WPMM) /
- window correlation matching method(WCMM)
Abstract: The Haikou Doppler radar volume scan composite elevation data and rainfall data from automatic meteorological rain gauges from Hainan Island collected from September to November in 2017—2018 was used to develop radar reflectivity Z and gauge rainfall R relationships (Z-R relationship) in various areas of Hainan Island for quantitative precipitation estimation by four matching methods: traditional matching method (TMM), probability matching method (PMM), window probability matching method (WPMM) and window correlation matching method (WCMM). And the errors of the four matching methods in hourly rainfall intensity and areal rainfall estimation were compared and analyzed. The results show that the four matching methods tend to overestimate the low rainfall events and underestimate the high rainfall events. The effect of rainfall estimation decreases with the increase of radar distance. PMM provides better result in estimating the Z-R relationships and much higher accuracy in quantitative estimation of precipitation than the other three matching methods. The mean absolute error of PMM in hourly rainfall intensity is less than 4 mm·h−1, and the minimum deviation of areal rainfall is only 2.1%.
| Citation: | DONG Lingyu, LIN Xiaobin, WENG Xiaofang. Comparative experiment of several quantitative precipitation estimation techniques based on doppler radar over the Hainan Island during autumn[J]. Journal of Tropical Biology, 2022, 13(4): 358-366. doi: 10.15886/j.cnki.rdswxb.2022.04.006 |




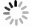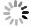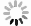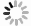
















 DownLoad:
DownLoad: